线段树概述
线段树是一种处理区间问题的优越算法,也是算法竞赛的常客。
线段树的特点是,类似于一棵二叉树,将一个序列分解成多个区间并储存在二叉树上。
例如,把区间$[1,10]$作为树的根节点,然后把$[1,5]$作为左子节点,把$[6,10]$作为右子节点,以此类推,不断扩散。
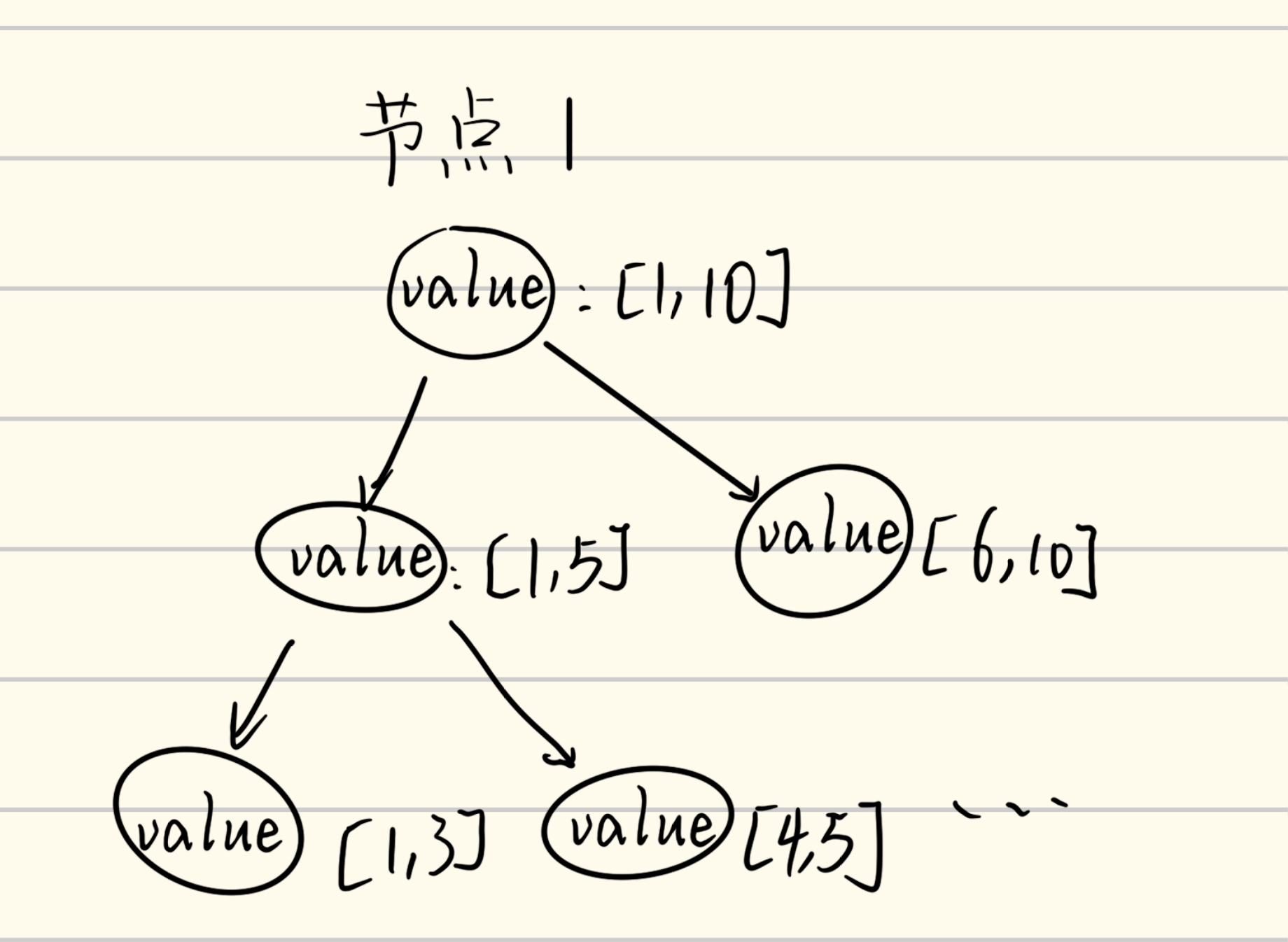
这种算法的优越之处在于每个节点都储存了某个区间的“特征值”。这个特征值可以是区间和,也可以是区间的最大值最小值。
我们知道,假如给定一个序列,需要求$m$次区间$[l,r]$的和,这个操作的时间复杂度是$O(mn)$。在算法竞赛中,$m,n>=10^5$的时候这个时间复杂度是不可以接受的。
而二叉树访问某个特定节点的时间复杂度是$O(logn)$,所以用线段树访问并维护区间“特征值”的时候,访问m次的时间复杂度只有$O(mlogn)$,极大降低了时间复杂度
也因此,线段树常常被用于解决某个区间可以被划分成子区间的问题,例如区间和,区间最值。
线段树的构造
接下来,我们看一下如何构造一个线段树。
类似二叉树,我们可以通过动态管理内存构造一棵二叉树,即通过结构体和指针动态分配二叉树的内存,也可以用一个静态数组构造一棵二叉树,在算法竞赛中,常用的是后者,本文也会以后者为示例。读者可以自行探索前一种写法。
正如我们前面所说,线段树需要维护的是区间的一个“特征值”,需要我们把这个特征值在构造线段树的时候计算出来存入,方便后续的调用。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
| #include<iostream>
#include<vector>
using namespace std;
#define ll long long
const int MAXN = 1e5+10;
ll tree[4*MAXN],a[MAXN];
int n,m;
void build(int index,int left,int right){
if(left==right){
tree[index]=a[left];
return;
}
int mid = left +(right-left)/2;
build(2*index,left,mid);
build(2*index+1,mid+1,right);
tree[index] = tree[2*index]+tree[2*index+1];
return;
}
|
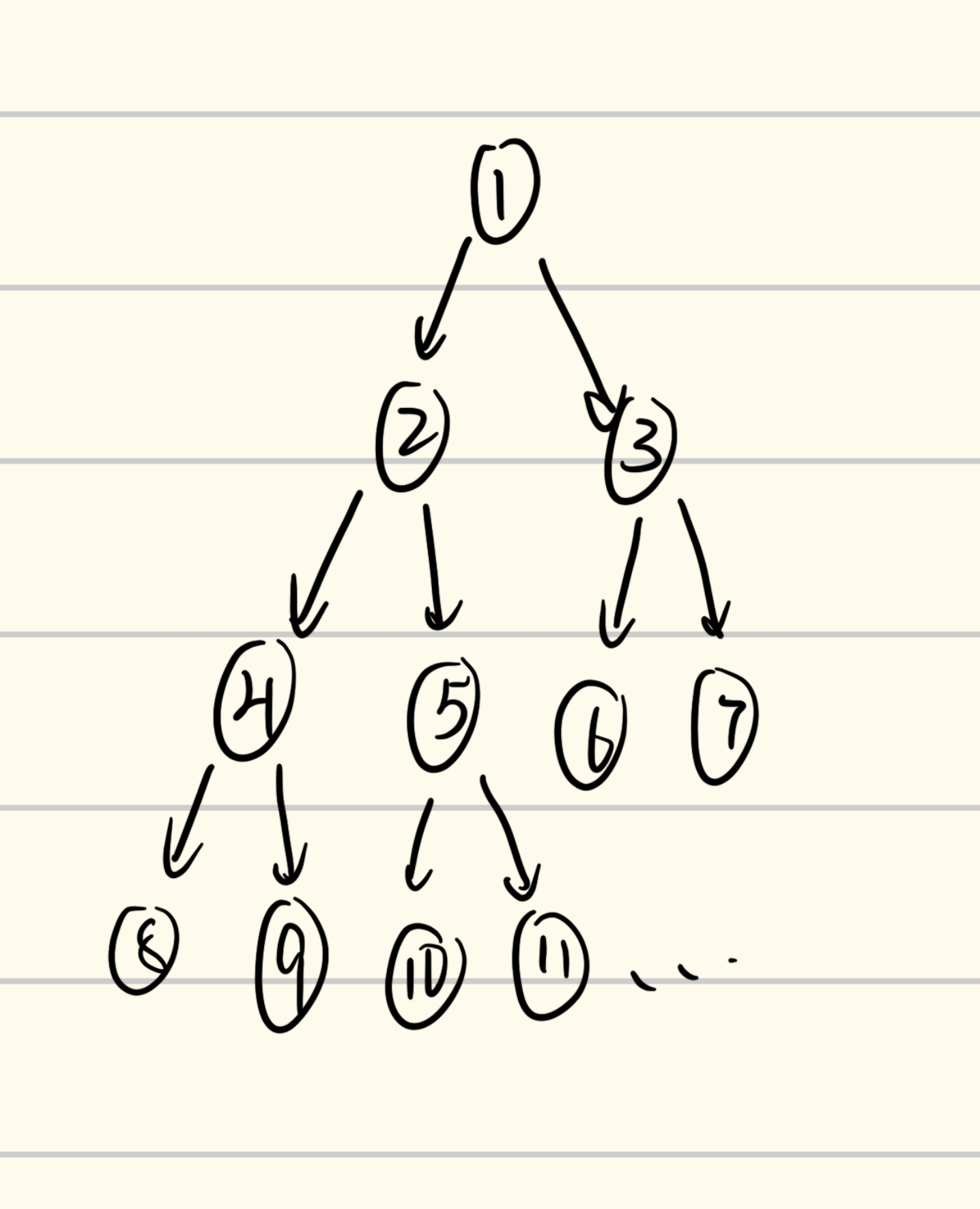
大致解释一下,假如我们给一棵满二叉树的节点从上到下、从左到右按顺序编号,那么节点$k$的左子节点必然是$2k$,右子节点必然是$2k+1$,这可以从数列的规律得到,在此不多阐述。
上面的代码就是通过递归,实现了先构造底层的区间和,上层节点直接把左区间和右区间的区间和加起来就得到了自己的区间和。
区间查询函数 query()
现在,我们已经知道一棵线段树如何构造了。
那么假如任务要求查询区间$[lb,rb]$的区间和,我们如何利用这棵线段树查询呢?
查询操作与构造类似,通过递归来计算区间[lb,rb]下有几个节点。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
| ll query(int index,int leftBound,int rightBound,int left,int right){
if(leftBound <= left&&rightBound>=right){
return tree[index];
}
int mid = left +(right-left)/2;
ll res=0;
if(leftBound<=mid){
res+= query(index<<1,leftBound,rightBound,left,mid);
}
if(mid+1<=rightBound){
res+= query(index<<1|1,leftBound,rightBound,mid+1,right);
}
return res;
}
调用:
query(1,l,r,1,n);
|
递归中,初始的区间必然大于等于查询区间,进入递归。
递归过程中有4种情况,一种是目前区间(A)在查询区间(B)内部,这种情况直接返回答案。
还有三种情况分别是A与B相交,A包含了B以及A与B互斥。
当AB互斥时,A与B无联系,不进入递归。
当A和B有重复的时候,A的某一个或几个子节点必然是在B内部的,因为A可以被拆分直到只剩一个元素。
所以我们要做的就是递归找到在B内部的A子节点,然后加入答案之中。
区间修改与懒标记(Lazy-Tag)
Lazy-Tag概述
试想,如果我们需要修改线段树上面的一个节点,时间复杂度是多少?
是O(logn),因为不仅需要修改这个节点,还需要修改这个节点的前驱全部节点(通过递归实现)
假如同时给一个区间[l,r]加10呢?那时间复杂度就取决于区间长度m,时间复杂度为O(mlogn)
这是不可忍受的时间复杂度,因为我们往往可能进行多次区间修改,总的时间复杂度会达到O(n^2logn)
Lazy-Tag就是解决这个问题的精妙构思。线段树的节点表示了这个区间的某个特征值,假如我们需要对这个区间整体操作,那么这个操作就可以被映射到特征值上面,而不必修改区间中的每个元素。
那么“懒”在哪?懒就懒在我们对根节点更新后,不必更新子节点,而是在下次递归的时候“顺路”把访问到的子节点更新了。它的本质是搭“顺风车”,这种思想并不少见,在效率最高的筛选素数方法:欧拉筛中,也是在循环中利用“搭顺风车”的办法减少时间复杂度。
总的来说,Lazy-Tag就是用一个tag[]数组,标记某个tree的节点需要被更新,并且在做其他操作,例如查询的时候顺便更新,减少时间复杂度。
区间修改
具体的修改思路是,对于给定的区间[l,r]的修改,先类似于查询,找出所有包含于[l,r]的节点,并且更新这些节点,再通过递归更新节点的上层节点。
这个过程中,我们并不关心区间[l,r]中的节点是否有子节点。例如, [3,5]在我们想要修改的区间[1,5]中,但我们不去修改[3,5]的子节点,因为那是懒标记做的事情
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
| void push_down(int index,int left,int right){
if(tag[index]){
int mid = left +(right-left)/2;
int ls=index*2,rs=index*2+1;
tag[ls]+=tag[index],tag[rs]+=tag[index];
tree[ls]+=(mid-left+1)*tag[index],tree[rs]+=(right-mid)*tag[index];
tag[index]=0;
}
}
void update(int index,int leftBound,int rightBound,int left,int right,ll value){
if(leftBound <= left&&rightBound>=right){
tree[index]+= (right-left+1)*value;
tag[index]+=value;
return;
}
push_down(index,left,right);
int mid = left +(right-left)/2;
ll res=0;
if(leftBound<=mid)
update(2*index,leftBound,rightBound,left,mid,value);
if(mid+1<=rightBound)
update(2*index+1,leftBound,rightBound,mid+1,right,value);
tree[index] = tree[index*2]+tree[index*2+1];
return;
}
|
这里的$tag[index]$表示已经对节点$index$修改过了,但是没有修改子节点
模板题
让我们通过一个模板题目把上面学到的知识串联起来吧。
P3372 【模板】线段树 1
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
| #include<iostream>
#include<vector>
using namespace std;
#define ll long long
const int MAXN = 1e5+10;
ll tree[4*MAXN],a[MAXN],tag[4*MAXN];
int n,m;
void build(int index,int left,int right){
if(left==right){
tree[index]=a[left];
return;
}
int mid = left +(right-left)/2;
build(2*index,left,mid);
build(2*index+1,mid+1,right);
tree[index] = tree[2*index]+tree[2*index+1];
return;
}
void push_down(int index,int left,int right){
if(tag[index]){
int mid = left +(right-left)/2;
int ls=index*2,rs=index*2+1;
tag[ls]+=tag[index],tag[rs]+=tag[index];
tree[ls]+=(mid-left+1)*tag[index],tree[rs]+=(right-mid)*tag[index];
tag[index]=0;
}
}
void update(int index,int leftBound,int rightBound,int left,int right,ll value){
if(leftBound <= left&&rightBound>=right){
tree[index]+= (right-left+1)*value;
tag[index]+=value;
return;
}
push_down(index,left,right);
int mid = left +(right-left)/2;
ll res=0;
if(leftBound<=mid)
update(2*index,leftBound,rightBound,left,mid,value);
if(mid+1<=rightBound)
update(2*index+1,leftBound,rightBound,mid+1,right,value);
tree[index] = tree[index*2]+tree[index*2+1];
return;
}
ll query(int index,int leftBound,int rightBound,int left,int right){
if(leftBound <= left&&rightBound>=right){
return tree[index];
}
push_down(index,left,right);
int mid = left +(right-left)/2;
ll res=0;
if(leftBound<=mid){
res+= query(index<<1,leftBound,rightBound,left,mid);
}
if(mid+1<=rightBound){
res+= query(index<<1|1,leftBound,rightBound,mid+1,right);
}
return res;
}
int main(){
cin>>n>>m;
for(int i=1;i<=n;i++)
cin>>a[i];
build(1,1,n);
for(int i=0;i<m;i++){
int op;
cin>>op;
if(op==2){
int l,r;
cin>>l>>r;
cout<<query(1,l,r,1,n)<<endl;
}else{
int l,r;long long val;
cin>>l>>r>>val;
update(1,l,r,1,n,val);
}
}
return 0;
}
|
补充练习
hdu 4027-Can you answer these queries?
hdu 4578-Transformation










