图的储存

储存图有很多种方式，在此介绍难度循序渐进的三种：邻接数组，邻接表，链式前向星。
第一种虽然简单，但访问的时间和空间花销过大，第三种最为优越，但使用较难，因此第二种最为常见。
让我们分别看看它们是什么

在介绍之前，我们先解释一下此处说的“图”是什么。

在算法领域，图一般指多个节点之间相互连接的关系。
这就是一个简单的图：

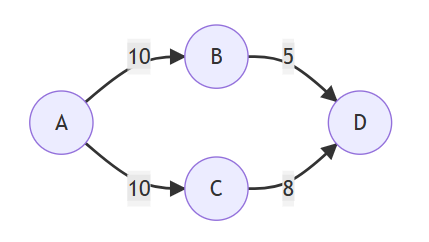
从上图可以看出，节点之间的联系可以是有向的，也可以是无向的，把图分为有向图和无向图。
节点之间的“边”可以是有长度的，也可以是无长度的，这里的长度一般被称为“权值”，把图分为有权图和无权图。
注意，权值并不一定是边的长度，也可以是和边有关的值，需要具体问题具体分析。

现在，我们来介绍一下如何储存这种点和边的关系。

邻接数组

这是最为简单的方法，使用一个二维数组去储存点和边的关系。
我们只考虑最复杂的有权有向图，至于其他类型，可以从有权有向图简化得到。如无权有向图就是把权值改为1即可。

现在用邻接数组储存 1->2，权值为3
和2->5，权值为6的两条边

1
2
3

p[1000][1000];
p[1][2]=3;
p[2][5]=6;

不难理解，一维下标就是出发节点，二维下标就是连接节点。
$p[i]$储存了所有与节点$i$相邻的边，由此得名邻接数组。

假如是无向边 1<->2，权值为3
和2<->5，权值为6，只需正反都存一次即可。可视作无向边就是从那个节点出发都可以抵达另一个节点。

p[1000][1000];
p[1][2]=3;
p[2][1]=3;
p[2][5]=6;
p[5][2]=6;

邻接表

可以看出，邻接表访问的时间复杂度极其夸张，尤其当边比较稀疏时。
如果有一万个节点，那么我想知道节点A连的边就要把$dp[A]$的一万个节点全部遍历一次，而其中很多次遍历都毫无意义。

因此，我们试想，有没有一种结构可以把所有边紧密的连接在一起呢？

邻接表正是这种数据结果。它用一种链式结构来储存边，只需要遍历这个链式结构即可。
一般我们使用$vector$来实现

vector<int> p[10000];//无权值边
//存入3->5,4->7
p[3].push_back(5);
p[4].push_back(7)
struct edge{
	int to;
	int len;
};
vector<edge> p[10000];//有权值边
//存入3->5,权值为8
p[3].push_back({5,8});

图的遍历

我们遍历一张图，通常采用DFS和BFS等方式。
我们需要根据具体问题，选择以什么方式遍历这张图能得到更好的答案。
例如，当问题需要遍历完一整个分支才能得到答案，优先选择DFS
而按层级优先的问题优先选择BFS。
~~DFS往往简单一点~~

P5318 【深基18.例3】查找文献

题目描述

小 K 喜欢翻看洛谷博客获取知识。每篇文章可能会有若干个（也有可能没有）参考文献的链接指向别的博客文章。小 K 求知欲旺盛，如果他看了某篇文章，那么他一定会去看这篇文章的参考文献（如果他之前已经看过这篇参考文献的话就不用再看它了）。

假设洛谷博客里面一共有 $n(n\le10^5)$ 篇文章（编号为 1 到 $n$）以及 $m(m\le10^6)$ 条参考文献引用关系。目前小 K 已经打开了编号为 1 的一篇文章，请帮助小 K 设计一种方法，使小 K 可以不重复、不遗漏的看完所有他能看到的文章。

这边是已经整理好的参考文献关系图，其中，文献 X → Y 表示文章 X 有参考文献 Y。不保证编号为 1 的文章没有被其他文章引用。

请对这个图分别进行 DFS 和 BFS，并输出遍历结果。如果有很多篇文章可以参阅，请先看编号较小的那篇(因此你可能需要先排序)。

输入格式

共 $m+1$ 行，第 1 行为 2 个数，$n$ 和 $m$，分别表示一共有 $n(n\le10^5)$ 篇文章（编号为 1 到 $n$）以及$m(m\le10^6)$ 条参考文献引用关系。

接下来 $m$ 行，每行有两个整数 $X,Y$ 表示文章 X 有参考文献 Y。

输出格式

共 2 行。
第一行为 DFS 遍历结果，第二行为 BFS 遍历结果。

输入输出样例 #1

输入 #1

输出 #1

1 2	1 2 5 6 3 7 8 4 1 2 3 4 5 6 7 8

题解：
这是一个比较简单的题目，要求我们使用两种方法遍历这个图，较为简单，可以作为大家了解图论的第一步。
遍历方法是DFS和BFS，DFS的大致思路是一直递归到尽头后返回，继续探索后面的支路。
BFS的大致思路是逐层遍历，把每层的节点轮流入队。
具体思路可见之前发布的文章。

#include<bits/stdc++.h>
using namespace std;
vector<int> p[100001];
int vis[100001];
void dfs(int now){
    vis[now]=1;
    vector<int>&temp=p[now];
    cout<<now<<" ";
    for(int& a:temp){
        if(vis[a]) continue;
        dfs(a);
    }
    return;
}
void bfs(const int& start){
    queue<int> q;
    q.push(start);
    cout<<start<<" ";
    vis[start]=1;
    while(q.size()){
        int now=q.front();//现在的文章的编号
        q.pop();
        for(auto&a:p[now]){//遍历每一个参考资料
            if(!vis[a]){
                cout<<a<<" ";
                vis[a]=1;
                q.push(a);
            }
        }
    }
}
int main(){
    int n,m;
    scanf("%d%d",&n,&m);
    for(int i=0;i<m;i++){
        int x,y;
        scanf("%d%d",&x,&y);
        vector<int>& temp=p[x];
        temp.push_back(y);
    }
    for(int i=1;i<=n;i++)
        sort(p[i].begin(),p[i].end());
    dfs(1);
    memset(vis,0,sizeof(vis));
    printf("\n");
    bfs(1);
    return 0;
}

P3916 图的遍历

题目描述

给出 $N$ 个点，$M$ 条边的有向图，对于每个点 $v$，求 $A(v)$ 表示从点 $v$ 出发，能到达的编号最大的点。

输入格式

第 $1$ 行 $2$ 个整数 $N,M$，表示点数和边数。

接下来 $M$ 行，每行 $2$ 个整数 $U_i,V_i$，表示边 $(U_i,V_i)$。点用 $1,2,\dots,N$ 编号。

输出格式

一行 $N$ 个整数 $A(1),A(2),\dots,A(N)$。

输入输出样例 #1

输入 #1

输出 #1

4 4 3 4

说明/提示

对于 $60\%$ 的数据，$1 \leq N,M \leq 10^3$。
对于 $100\%$ 的数据，$1 \leq N,M \leq 10^5$。

题解：
此题很明显需要用DFS，因为需要遍历完整个分支才能得到答案。

但是DFS遍历有两个劣势。第一个是非常容易超时，尤其是已经在已经访问过的节点需要重复访问的时候。

面对第一个问题，可以尝试记忆化搜索，也就是DFS+DP。

记忆化搜索的思路是，我把每个点可以到达的最大值记录下来，再return给上层的点知道。

这样下次需要遍历这个结构的时候，我只需要调用记录好的最大值就可以了，非常方便。

但是此题并不是有向无环图（DAG）。有环形结构，就会导致DFS在获取下层点数据的时候，返回会获取到上层点（请读者自行构想一个环形结构）
因此无法记忆化搜索。

那么如何避免这个问题？

既然找最大点那么麻烦，那就让最大点去找子结构吧！

这样我们只需要遍历整张图一次就可以，因为从大点开始遍历它的上层点的话，剩余的小点必定无法影响这个结果，不需要重复遍历。

也因此，我们需要反向建有向边，更便于大点去找上层结构。

#include<bits/stdc++.h>
using namespace std;
const int MAXN=100005;
int n,m;
vector<int> points[MAXN];
bool vis[MAXN];
int maxs[MAXN];

void dfs(int start,int now){
    vector<int>& nowTos=points[now];
    vis[now]=1;
    for(int i=0,len=nowTos.size();i<len;i++){
        if(vis[nowTos[i]]){
            continue;
        }
        maxs[nowTos[i]]=start;
        dfs(start,nowTos[i]);
    }
    
}

int main(){
    cin>>n>>m;
    for(int i=0;i<m;i++){
        int x,y;
        cin>>x>>y;
        points[y].push_back(x);
    }
    for(int i=1;i<=n;i++)
        maxs[i]=i;
    for(int i=n;i>=1;i--){//让大点先去告诉子点，这样既不关心路径尽头是不是环形
                          //（因为更新的值是一开始就注定的），也不用处理其他点dfs的遍历，因为越大的点优先级越高，从n遍历到1即可
        dfs(i,i);
        
    }
    for(int i=1;i<=n;i++)
        cout<<maxs[i]<<" ";
    return 0;
}

记忆化搜索

P1113 杂务

思路：

分析题目可知，此为有向无环图（DAG）

每项任务完成的最短时间，必定是前驱任务中最长时间的一项加上完成本项任务本身（其他快于最长前驱任务的可以同时完成）

而前驱任务的时长也可由此得出，并且满足动态规划的无后效性和最优子结构，故可以尝试DFS+dp记忆化搜索。

递推方程是 $dp[i] = dp[i] + max(dp[i的子节点])$

经过上面的分析，我们发现让前置任务较多的任务位于树形结构的上层更有利于DFS，（可以直接在循环内去找下层最大值）因此也采用反向建边的策略。

代码如下：

#include<bits/stdc++.h>
using namespace std;
const int MAXN=10005;
vector<int> points[MAXN];
int vis[MAXN];
int dp[MAXN];
int n;
int totoalMax=0;
void dfs(int i){//遍历下层，维护下层最大值，然后加上
    vector<int>& tos=points[i];
    int maxNum=0;
    for(int i=0,sz=tos.size();i<sz;i++){
        if(vis[tos[i]]){
            maxNum=max(dp[tos[i]],maxNum);
            continue;
        }
        dfs(tos[i]);
    }
    dp[i]+=maxNum;
    totoalMax=max(totoalMax,dp[i]);
    vis[i]=1;
    return;
}

int main(){
    cin>>n;
    for(int i=1;i<=n;i++){
        int x,xt;
        cin>>x>>xt;
        dp[x]=xt;//初始化时间
        int temp;
        cin>>temp;
        while(temp){//建temp到x的反向边，防备反向遍历
            points[temp].push_back(x);
            cin>>temp;
        }
    }
    for(int i=n;i>0;i--){
        dfs(i);
    }
    cout<<totoalMax;
    return 0;
}

补充练习： P4017 最大食物链计数

题目背景

你知道食物链吗？Delia 生物考试的时候，数食物链条数的题目全都错了，因为她总是重复数了几条或漏掉了几条。于是她来就来求助你，然而你也不会啊！写一个程序来帮帮她吧。

题目描述

给你一个食物网，你要求出这个食物网中最大食物链的数量。

（这里的“最大食物链”，指的是生物学意义上的食物链，即最左端是不会捕食其他生物的生产者，最右端是不会被其他生物捕食的消费者。）

Delia 非常急，所以你只有 $1$ 秒的时间。

由于这个结果可能过大，你只需要输出总数模上 $80112002$ 的结果。

输入格式

第一行，两个正整数 $n、m$，表示生物种类 $n$ 和吃与被吃的关系数 $m$。

接下来 $m$ 行，每行两个正整数，表示被吃的生物A和吃A的生物B。

输出格式

一行一个整数，为最大食物链数量模上 $80112002$ 的结果。

输入输出样例 #1

输入 #1

输出 #1

说明/提示

各测试点满足以下约定：

【补充说明】

数据中不会出现环，满足生物学的要求。（感谢 @AKEE ）
本题仍然满足有向无环图，可以用与上题类似的思路解决，不过多赘述。

另外，本题数据规模较大，但记忆化搜索可以轻松通过，可见其在时间复杂度上的优越性。

代码：

#include<bits/stdc++.h>
using namespace std;
const int MOD=80112002;
const int MAXN=5005;
vector<int> p[MAXN];
int vis[MAXN],dp[MAXN];
int n,m,ans;
int dfs(int now){
    if(dp[now])
        return dp[now];
    vector<int>& tos=p[now];
    int len=tos.size();
    int tempAns=0;
    if(len==0){
        dp[now]=1;
        return 1;
    }
    for(int i=0;i<len;i++){
        tempAns=(tempAns+dfs(tos[i])%MOD)%MOD;
    }
    dp[now]=tempAns;
    return tempAns;
}
//寻找0入度的点：主函数循环+vis数组
int main(){
    cin>>n>>m;
    for(int i=0;i<m;i++){
        int a,b;
        cin>>a>>b;
        //b吃a
        vis[a]=1;
        p[b].push_back(a);
    }
    for(int i=1;i<=n;i++){//无法确保1是0入度的
        if(vis[i])
            continue;
        ans=(ans+dfs(i)%MOD)%MOD;
    }
    cout<<ans;
    return 0;
}